• Cryptography
• Elliptic Curve Cipher And ECDSA

Elliptic Curve Cipher And ECDSA

This topic is finally relevant to Blockchain!! We get there!!

If you skipped the other parts, I still think other parts are still crucial to understand.

ECC (Elliptic Curve Cipher) uses smaller key than RSA, but provides the same level of security and speed.

ECC keys

The key generation is very simple, just to generate a random integer in a certain range. e.g. any number that is under 256 bits (which is a very large range, impossible to brute-forcefully crack the private key to yield the same result unless it is already known).

The public key in the ECC is laying on {x, y} on the curve (EC points) and this point can be compressed into one coordinates plus one bit (even or odd). Hence if the private key is 256 bits, the public key will be 257 bits.

Curves

Different curves could be used by different ECC algos, which differs themselves from security, key length and performance.

Each ECC curves have their own names (e.g. secp256k1), field-size (e.g. 256-bit), and other params.

ECC Maths

This page gave us a full form of elliptic curve, but it could be simplified like this:

y^2 = x^3 + a x + b

e.g. The NIST curve secp256k1 used in Bitcoin use the curve

y^2 = x^3 + 7

where a = 0, b = 7.

Here's a desmos that can makes you play with the curve.

ECC Maths in practice

In practice, the ECC curve will be taken to a finite field, that will mod the result of EC with a certain number p, so that there is only p number of points on the EC.

EC point multiplication

Wikipedia actually help me understand the EC. Before you understand EC point multiplication, you need to understand point addition and point doubling.

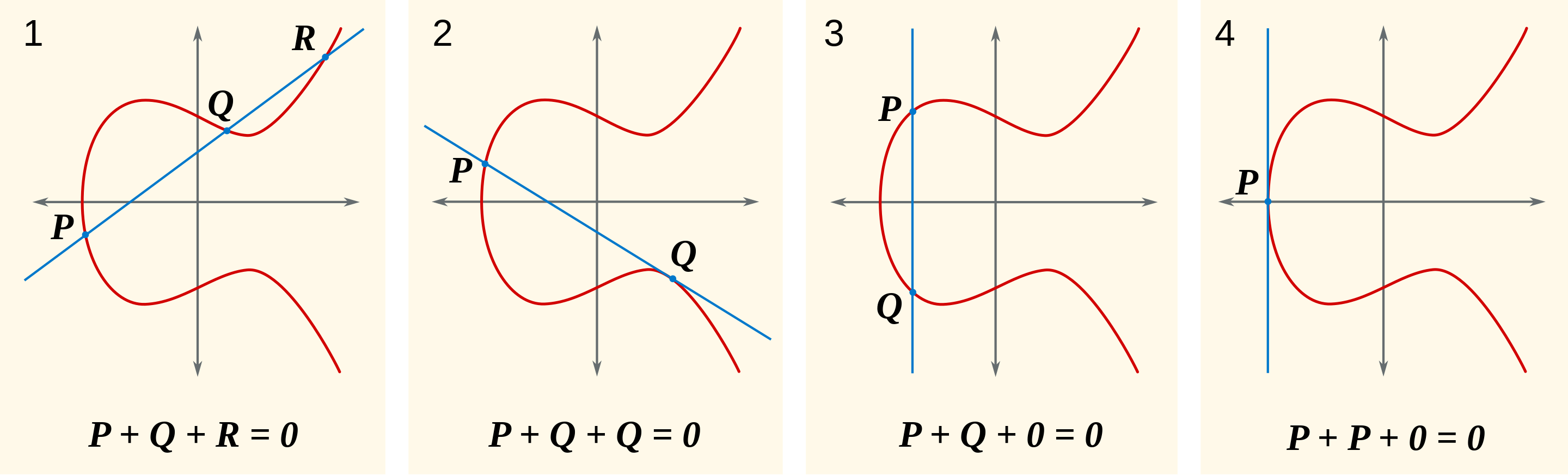
Point addition & doubling

Point multiplication

This [section] list out different algo of computing the multiplication.

The simplest method to understand is the "Double-And-Add" method (to compute K = k * G):

let bits = bit_representation(k)
let res = math.inf

let temp = G # track doubled P val
for bit in bits:
    if bit == 1:
        res = res + temp # point add
    temp = temp + temp # double
return res

We can see the algorithm just does very simple stuffs: iteractively add (on odd bits) and double (on even bits).

Properties of EC point multiplication

There are two properties of EC point multiplication: K = k * G:

EC subgroups and co-factors

Suppose there are n = r * h points on a finite-field EC, there are only h number of non-overlapping subgroups (each group contains r points).

h is also called the "co-factors" of an EC curve. r is also called the "order" of an EC curve.

• Example of elliptic curve having cofactor = 1 is secp256k1
• Example of elliptic curve having cofactor = 8 is Curve25519
• Example of elliptic curve having cofactor = 4 is Curve448

Apply EC point multiplication to PKC

Using the EC point multiplication property, we can easily determine that, given a formula K = k * G:

This section tells us how scientists carefully selects the generator G.

To summarize, in the ECC cryptography the EC points, together with the generator point G form cyclic groups (or cyclic subgroups), which means that a number r exists (r > 1), such that r * G = 0 * G = infinity and all points in the subgroup can be obtained by multiplying G by integer in the range [1...r]. The number r is called order of the group (or subgroup).

EC could have many generator G, but we only need to pick one to make sure the performance and security is optimized.

Different G also yields subgroups of different order. We need to make sure the order r is large enough to defend the small subgroup attack. And this r needs to be a prime number.

Key length strength and security

Because the fastest known algorithm to solve the ECDLP for key of size k needs sqrt(k) steps, this means that to achieve a k-bit security strength, at least 2^k-bit curve is needed. Thus 256-bit elliptic curves (where the field size p is 256-bit number) typically provide nearly 128-bit security strength.

from cryptobook

Public Key Compression

Another important property of EC is that there are at most 2 coordinates that exists given same y (odd x and even x). See this section. That's why the public key only needs the x coordinates and plus one bit with odd or even.

ECDSA

The process of ECDSA is similar to RSA, using the private key to sign and using the public key to verify.

ECDSA Sign

1. compute message hash h using hash function like SHA-256: h = hash(msg)
2. generate a cryptographically secure random number k in the range of [1,n-1]
   • note that this is not the private key k we mentioned before!!! but it should be kept secret too
   • every signature should choose a different k so that keys are not easily figured out
   • for deterministic-ECDSA, the value k is HMAC-derived from h + privKey (this is to make sure given the same msg, the signatures are the same)
3. calculate R = k * G and extract x coordinate of R: r = R.x
4. calculate the signature proof: s = k^-1 * (h + r * privKey) mod n
   • k * k^-1 = 1 mod n
5. return the signature {r, s}

In summary:

The signing encodes a random point R (represented by its x-coordinate only) through elliptic-curve transformations using the private key privKey and the message hash h into a number s, which is the proof that the message signer knows the private key privKey. The signature {r, s} cannot reveal the private key due to the difficulty of the ECDLP problem.

ECDSA Verify

Suppose signature {r, s} and original message are given, all you need to do is to recover the random point r from the result s and pubKey to learn about if the signature is from the key holder.

1. compute message hash h using hash function like SHA-256: h = hash(msg)
2. modular reverse the signature s: s' = s^-1 mod n
3. recover the random point by R' = (h * s') * G + (r * s') * pubKey
4. take the r': r' = R'.x
5. compare whether r' == r, if they are not the same, the signature is not from the key holder!

In summary:

The signature verification decodes the proof number s from the signature back to its original point R , using the public key pubKey and the message hash h and compares the x-coordinate of the recovered R with the r value from the signature.

The Math

This section gives the math proof why the verification is valid. In short, it's all math substitutions and the simplifications.

ECDSA Public Key Recovery from Signature

ECDSA allows the public key to be recovered from the {r,s}, and returns 0, 1 and 2 possible EC points that could be valid public keys, so to avoid the ambiguity, the signature need to have one extra bit v, so the signature become {r,s,v}.

Wikipedia explained how that is done.

Major Malleability

This article explains how one could fake the signature:

Suppose we sign the message:

const signature = key.sign(msgHash);

The result is going to be {r,s}

But, we can use two signatures to potentially pass the validation:

{r, s}

{r, -s mod n}

n is the size of the range of a random number, which could be derived from the EC. Hence the second result could be derived

That's why the verification algo should also verify whether it's the lower s.

A lot of programming languages' native crypto library might not have such verification, including Solidity. That's why one should use OZ's util library to verify signature.

They have a line of code checking whether s is the lower s:

if (uint256(s) > 0x7FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF5D576E7357A4501DDFE92F46681B20A0) {
  return (address(0), RecoverError.InvalidSignatureS);
}